SEGUNDO CASO
1.- Un ascensor pesa 400 Kp. ¿Qué fuerza debe ejercer el cable hacia arriba para que suba con una aceleración de 5 m/s2? Suponiendo nulo el roce y la masa del ascensor es de 400 Kg.
Solución
Como puede verse en la figura 7, sobre el ascensor actúan dos fuerzas: la fuerza F de tracción del cable y la fuerza P del peso, dirigida hacia abajo.

La fuerza resultante que actúa sobre el ascensor es F – P
Aplicando la ecuación de la segunda ley de Newton tenemos:

Si despejamos F tenemos:
F = 200 N + 3920 N
F = 4120 N
2.- Un carrito con su carga tiene una masa de 25 Kg. Cuando sobre él actúa, horizontalmente, una fuerza de 80 N adquiere una aceleración de 0,5 m/s2. ¿Qué magnitud tiene la fuerza de rozamiento Fr que se opone al avance del carrito?
Solución
En la figura 8 se muestran las condiciones del problema
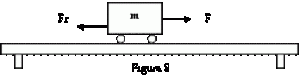
La fuerza F, que actúa hacia la derecha, es contrarrestada por la fuerza de roce Fr, que actúa hacia la izquierda. De esta forma se obtiene una resultante F – Fr que es la fuerza que produce el movimiento.
Si aplicamos la segunda ley de Newton se tiene:
Si despejamos Fr nos queda:
Fr = 80 N – 12,5 N
Fr = 67,5 N
3.- ¿Cuál es la fuerza necesaria para que un móvil de 1500 Kg., partiendo de reposo adquiera una rapidez de 2 m/s2 en 12 s?
Datos
F =?
m = 1500 Kg.
Vo = 0
Vf = 2 m/s2
t = 12 s
Solución
Como las unidades están todas en el sistema M.K.S. no necesitamos hacer transformaciones.
La fuerza que nos piden la obtenemos de la ecuación de la segunda ley de Newton:
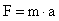

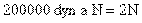
1.- Un ascensor pesa 400 Kp. ¿Qué fuerza debe ejercer el cable hacia arriba para que suba con una aceleración de 5 m/s2? Suponiendo nulo el roce y la masa del ascensor es de 400 Kg.
Solución
Como puede verse en la figura 7, sobre el ascensor actúan dos fuerzas: la fuerza F de tracción del cable y la fuerza P del peso, dirigida hacia abajo.

La fuerza resultante que actúa sobre el ascensor es F – P
Aplicando la ecuación de la segunda ley de Newton tenemos:

400 Kp = 400 x 9,8 N = 3920 N
Sustituyendo los valores de P, m y a se tiene:
F – 3920 N = 400 Kg. x 0,5 m/s2
F – 3920 N = 200 N
Si despejamos F tenemos:
F = 200 N + 3920 N
F = 4120 N
2.- Un carrito con su carga tiene una masa de 25 Kg. Cuando sobre él actúa, horizontalmente, una fuerza de 80 N adquiere una aceleración de 0,5 m/s2. ¿Qué magnitud tiene la fuerza de rozamiento Fr que se opone al avance del carrito?
Solución
En la figura 8 se muestran las condiciones del problema

La fuerza F, que actúa hacia la derecha, es contrarrestada por la fuerza de roce Fr, que actúa hacia la izquierda. De esta forma se obtiene una resultante F – Fr que es la fuerza que produce el movimiento.
Si aplicamos la segunda ley de Newton se tiene:
Sustituyendo F, m y a por sus valores nos queda
80 N – Fr = 25 Kg. x 0,5 m/s2
80 N – Fr = 12,5 N
Si despejamos Fr nos queda:
Fr = 80 N – 12,5 N
Fr = 67,5 N
3.- ¿Cuál es la fuerza necesaria para que un móvil de 1500 Kg., partiendo de reposo adquiera una rapidez de 2 m/s2 en 12 s?
Datos
F =?
m = 1500 Kg.
Vo = 0
Vf = 2 m/s2
t = 12 s
Solución
Como las unidades están todas en el sistema M.K.S. no necesitamos hacer transformaciones.
La fuerza que nos piden la obtenemos de la ecuación de la segunda ley de Newton:
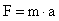
De esa ecuación conocemos la masa, pero desconocemos la aceleración. Esta podemos obtenerla a través de la ecuación
Porque partió de reposo.
Sustituyendo Vf y t por sus valores tenemos:
Si sustituimos el valor de a y de m en la ecuación (I) tenemos que:
F= 1500 Kg x 0,16 m/s2
F= 240 N
4.- ¿Qué aceleración adquirirá un cuerpo de 0,5 Kg. cuando sobre él actúa una fuerza de 200000 dinas?
Datos
a =?
m = 2,5 Kg.
F = 200000 dyn
Solución
La masa está dada en M.K.S., en cambio la fuerza está dada en c.g.s.
Para trabajar con M.K.S. debemos transformar la fuerza a la unida M.K.S. de esa magnitud (N)

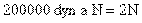
La ecuación de la segunda ley de Newton viene dada por:
Despejando a tenemos:
Sustituyendo sus valores se tiene:
TERCER CASO
1.- Dos niños, Juan de 20kg y Pedro de 25kg, están frente a frente en una pista de hielo. Juan da un empujón a Pedro y este sale despedido con una rapidez de 3m/seg. Calcular la rapidez con que retrocede Juan, suponiendo que los patines no ofrecen resistencia al movimiento
Razonamiento: En un caso de la ley de acción y reacción, por lo tanto, aplicamos la fórmula correspondiente, si es necesario despejamos, y sustituimos valores en un sistema de medidas.
Datos:
m1 = 20kg
m2 = 25kg
v1 = 3m/seg
v2 = ?
Despejamos:
m1 x v1 = m2 x v2 } v1 = m2 x v2
m1
Resolvemos:
v1 = 25kg x 3m/seg = 3,75m/seg
20kg
2.- Dos niños están patinando sobre una pista de hielo. Se empujan y salen despedidos con velocidades de 3m/seg y 3,5m/seg. Si la masa del primer niño es de 25kg, calcular la masa del segundo.
Datos:
v1 = 3m/seg
v2 = 3,5m/seg
m1 = 25kg
m2 = ?
Formula que utilizaremos:
m2= m1 x v1
v2
Resolvemos:
m2= 25kg x 3m/seg = 21,42kg
3,5m/seg
3.- El dibujo representa a dos cuerpo, A y B, unidos por una cuerda a través de una polea. El cuerpo A está situado sobre una superficie horizontal y e cuerpo B cuelga libremente de la polea. Si hay fuerza de rozamiento sobre A, hacer un diagrama de cuerpo libre de cada uno de ellos.
Cuerpo A
sobre el cuerpo A actúan las siguientes fuerzas:
Pa = es el peso del cuerpo A
Na = es la fuerza con que la superficie actúa sobre la A
T = es la tensión de la cuerda
Fr = es la fuerza de rozamiento entre la superficie y la A
Cuerpo B
Sobre el cuerpo B actúan las siguientes fuerzas:
Pb = es el peso del cuerpo B
T = es la tensión de la cuerda
4.- El dibujo representa a dos cuerpos, A y B, unidos por una cuerda a través de una polea. El cuerpo A está situado sobre una superficie inclinada y el B cuelga libremente de la polea. Si hay fuerza de rozamiento sobre A, hacer un diagrama de cuerpo libre de cada uno de ellos
Las fuerzas que actúan sobre un cuerpo se sitúan sobre un sistema de coordenadas el cual se orientan para facilitar los cálculos
En este caso para, para el cuerpo A, el eje X lo dibujamos paralelo al plano inclinado
Cuerpo A
Las fuerzas que actúan sobre el cuerpo A son:
T = es la tensión de la cuerda
Pa = es el peso del cuerpo A
Na = es la fuerza normal con que la superficie acciona al cuerpo
Fr = es la fuerza de rozamiento
Cuerpo B
Las fuerzas que actúan sobre el cuerpo B son:
Pb = es el peso de la cuerda B
T = es la tensión de la cuerda
Sobre el cuerpo B actúan las siguientes fuerzas:
Pb = es el peso del cuerpo B
T = es la tensión de la cuerda
4.- El dibujo representa a dos cuerpos, A y B, unidos por una cuerda a través de una polea. El cuerpo A está situado sobre una superficie inclinada y el B cuelga libremente de la polea. Si hay fuerza de rozamiento sobre A, hacer un diagrama de cuerpo libre de cada uno de ellos
Las fuerzas que actúan sobre un cuerpo se sitúan sobre un sistema de coordenadas el cual se orientan para facilitar los cálculos
En este caso para, para el cuerpo A, el eje X lo dibujamos paralelo al plano inclinado
Cuerpo A
Las fuerzas que actúan sobre el cuerpo A son:
T = es la tensión de la cuerda
Pa = es el peso del cuerpo A
Na = es la fuerza normal con que la superficie acciona al cuerpo
Fr = es la fuerza de rozamiento
Cuerpo B
Las fuerzas que actúan sobre el cuerpo B son:
Pb = es el peso de la cuerda B
T = es la tensión de la cuerda

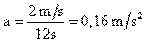


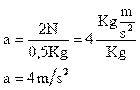







Comentarios
Publicar un comentario